Here’s a very pretty problem I encountered on Twitter from Mike Lawler 1.5 months ago.
I’m late to the game replying to Mike’s post, but this problem is the most lovely combination of features of quadratic and trigonometric functions I’ve ever encountered in a single question, so I couldn’t resist. This one is well worth the time for you to explore on your own before reading further.
My full thoughts and explorations follow. I have landed on some nice insights and what I believe is an elegant solution (in Insight #5 below). Leading up to that, I share the chronology of my investigations and thought processes. As always, all feedback is welcome.
WARNING: HINTS AND SOLUTIONS FOLLOW
Investigation #1:
My first thoughts were influenced by spoilers posted as quick replies to Mike’s post. The coefficients of the underlying quadratic, 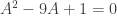 , say that the solutions to the quadratic sum to 9 and multiply to 1. The product of 1 turned out to be critical, but I didn’t see just how central it was until I had explored further. I didn’t immediately recognize the 9 as a red herring.
, say that the solutions to the quadratic sum to 9 and multiply to 1. The product of 1 turned out to be critical, but I didn’t see just how central it was until I had explored further. I didn’t immediately recognize the 9 as a red herring.
Basic trig experience (and a response spoiler) suggested the angle values for the tangent embedded in the quadratic weren’t common angles, so I jumped to Desmos first. I knew the graph of the overall given equation would be ugly, so I initially solved the equation by graphing the quadratic, computing arctangents, and adding.
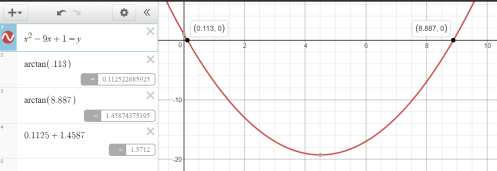
Insight #1: A Curious Sum
The sum of the arctangent solutions was about 1.57…, a decimal form suspiciously suggesting a sum of 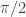 . I wasn’t yet worried about all solutions in the required
. I wasn’t yet worried about all solutions in the required ![[0,2\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002) interval, but for whatever strange angles were determined by this equation, their sum was strangely pretty and succinct. If this worked for a seemingly random sum of 9 for the tangent solutions, perhaps it would work for others.
interval, but for whatever strange angles were determined by this equation, their sum was strangely pretty and succinct. If this worked for a seemingly random sum of 9 for the tangent solutions, perhaps it would work for others.
Unfortunately, Desmos is not a CAS, so I turned to GeoGebra for more power.
Investigation #2:
In GeoGebra, I created a sketch to vary the linear coefficient of the quadratic and to dynamically calculate angle sums. My procedure is noted at the end of this post. You can play with my GeoGebra sketch here.
The x-coordinate of point G is the sum of the angles of the first two solutions of the tangent solutions.
Likewise, the x-coordinate of point H is the sum of the angles of all four angles of the tangent solutions required by the problem.

Insight #2: The Angles are Irrelevant
By dragging the slider for the linear coefficient, the parabola’s intercepts changed, but as predicted in Insights #1, the angle sums (x-coordinates of points G & H) remained invariant under all Real values of points A & B. The angle sum of points C & D seemed to be 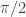 (point G), confirming Insight #1, while the angle sum of all four solutions in
(point G), confirming Insight #1, while the angle sum of all four solutions in ![[0,2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi%5D&bg=ffffff&fg=333333&s=0&c=20201002) remained
remained 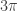 (point H), answering Mike’s question.
(point H), answering Mike’s question.
The invariance of the angle sums even while varying the underlying individual angles seemed compelling evidence that that this problem was richer than the posed version.
Insight #3: But the Angles are bounded
The parabola didn’t always have Real solutions. In fact, Real x-intercepts (and thereby Real angle solutions) happened iff the discriminant was non-negative: 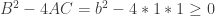 . In other words, the sum of the first two positive angles solutions for
. In other words, the sum of the first two positive angles solutions for 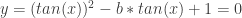 is
is 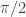 iff
iff  , and the sum of the first four solutions is
, and the sum of the first four solutions is 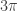 under the same condition. These results extend to the equalities at the endpoints iff the double solutions there are counted twice in the sums. I am not convinced these facts extend to the complex angles resulting when
under the same condition. These results extend to the equalities at the endpoints iff the double solutions there are counted twice in the sums. I am not convinced these facts extend to the complex angles resulting when 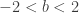 .
.
I knew the answer to the now extended problem, but I didn’t know why. Even so, these solutions and the problem’s request for a SUM of angles provided the insights needed to understand WHY this worked; it was time to fully consider the product of the angles.
Insight #4: Finally a proof
It was now clear that for  there were two Quadrant I angles whose tangents were equal to the x-intercepts of the quadratic. If
there were two Quadrant I angles whose tangents were equal to the x-intercepts of the quadratic. If 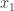 and
and  are the quadratic zeros, then I needed to find the sum A+B where
are the quadratic zeros, then I needed to find the sum A+B where 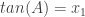 and
and  .
.
From the coefficients of the given quadratic, I knew 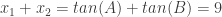 and
and 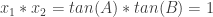 .
.
Employing the tangent sum identity gave
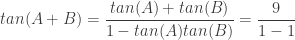
and this fraction is undefined, independent of the value of  as suggested by Insight #2. Because tan(A+B) is first undefined at
as suggested by Insight #2. Because tan(A+B) is first undefined at 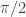 , the first solutions are
, the first solutions are  .
.
Insight #5: Cofunctions reveal essence
The tangent identity was a cute touch, but I wanted something deeper, not just an interpretation of an algebraic result. (I know this is uncharacteristic for my typically algebraic tendencies.) The final key was in the implications of 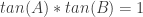 .
.
This product meant the tangent solutions were reciprocals, and the reciprocal of tangent is cotangent, giving
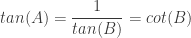 .
.
But cotangent is also the co-function–or complement function–of tangent which gave me
 .
.
Because tangent is monotonic over every cycle, the equivalence of the tangents implied the equivalence of their angles, so  , or
, or 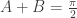 . Using the Insights above, this means the sum of the solutions to the generalization of Mike’s given equation,
. Using the Insights above, this means the sum of the solutions to the generalization of Mike’s given equation,
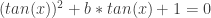 for x in
for x in ![[0,2\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002) and any
and any  ,
,
is always 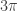 with the fundamental reason for this in the definition of trigonometric functions and their co-functions. QED
with the fundamental reason for this in the definition of trigonometric functions and their co-functions. QED
Insight #6: Generalizing the Domain
The posed problem can be generalized further by recognizing the period of tangent:  . That means the distance between successive corresponding solutions to the internal tangents of this problem is always
. That means the distance between successive corresponding solutions to the internal tangents of this problem is always  each, as shown in the GeoGebra construction above.
each, as shown in the GeoGebra construction above.
Insights 4 & 5 proved the sum of the angles at points C & D was 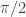 . Employing the periodicity of tangent, the x-coordinate of
. Employing the periodicity of tangent, the x-coordinate of 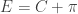 and
and 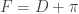 , so the sum of the angles at points E & F is
, so the sum of the angles at points E & F is  .
.
Extending the problem domain to ![[0,3\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2C3%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002) would add
would add 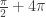 more to the solution, and a domain of
more to the solution, and a domain of ![[0,4\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2C4%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002) would add an additional
would add an additional 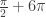 . Pushing the domain to
. Pushing the domain to ![[0,k\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2Ck%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002) would give total sum
would give total sum
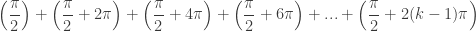
Combining terms gives a general formula for the sum of solutions for a problem domain of ![[0,k\pi ]](https://s0.wp.com/latex.php?latex=%5B0%2Ck%5Cpi+%5D&bg=ffffff&fg=333333&s=0&c=20201002)
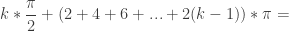
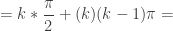
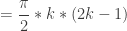
For the first solutions in Quadrant I, ![[0,\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cpi%5D&bg=ffffff&fg=333333&s=0&c=20201002) means k=1, and the sum is
means k=1, and the sum is 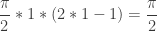 .
.
For the solutions in the problem Mike originally posed, ![[0,2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5Cpi%5D&bg=ffffff&fg=333333&s=0&c=20201002) means k=2, and the sum is
means k=2, and the sum is  .
.
I think that’s enough for one problem.
APPENDIX
My GeoGebra procedure for Investigation #2:
- Graph the quadratic with a slider for the linear coefficient,
 .
.
- Label the x-intercepts A & B.
- The x-values of A & B are the outputs for tangent, so I reflected these over y=x to the y-axis to construct A’ and B’.
- Graph y=tan(x) and construct perpendiculars at A’ and B’ to determine the points of intersection with tangent–Points C, D, E, and F in the image below
- The x-intercepts of C, D, E, and F are the angles required by the problem.
- Since these can be points or vectors in Geogebra, I created point G by G=C+D. The x-intercept of G is the angle sum of C & D.
- Likewise, the x-intercept of point H=C+D+E+F is the required angle sum.

can be expressed two ways: as the sum of the areas of the isosceles triangles, and using Heron’s formula. From the areas of the isosceles triangles,
are 2x, 2y, and 2z, so its semiperimeter is x+y+z and Heron’s formula gives its area as
.







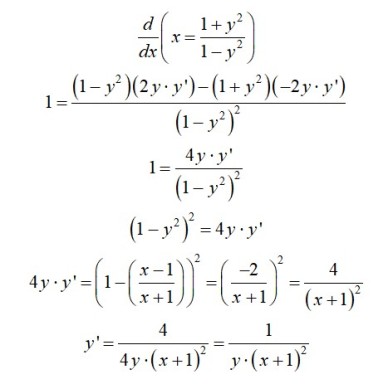


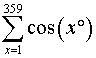 is the gold nugget in the assignment, especially with your students’ prior exposure to special angles.
is the gold nugget in the assignment, especially with your students’ prior exposure to special angles. ?
? , with sine or cosine.
, with sine or cosine.