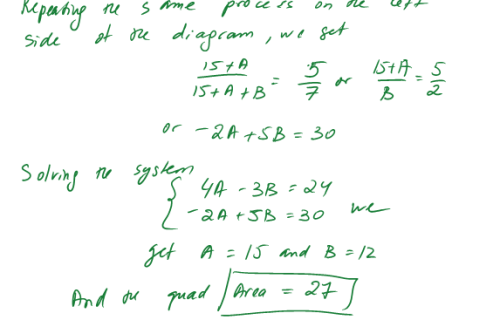Pythagorean Investigation

 

Here’s a challenge @jamestanton tweeted yesterday:

Can the hypotenuse and one side length of one right integer triangle be the two side lengths of another right integer triangle?

— James Tanton (@jamestanton) September 9, 2018

Visually, Tanton is asking if there is an integer right triangle (like the standard version shown on the left below) for which the integer triangle on the right exists.

The algebraic equivalent to this question is, for some , does there exist a Natural number d so that ?

I invoked Euclid’s formula in my investigation to show that there is no value of d to make this possible.  I’d love to hear of any other proof variations.

INVOKING EUCLID’S FORMULA

For any coprime natural numbers m & n where and is odd, then every primitive Pythagorean triple can be generated by .

For any Natural number k, every Pythagorean triple can be generated by .

The generator term must be the original hypotenuse (side c), but either or can be side b.  So, if Tanton’s scenario is true, I needed to check two possible cases.  Does there exist a Natural number d such that

or

is true?

EVALUATING THE POSSIBILITIES

For the first equation, there is a single factor of 2 on the right, and there is no way to extract an odd number of factors of 2 from or , so can’t represent a perfect square.

For the second equation, there is no way to factor over Integers, so can’t be a perfect square either.

Since neither equation can create a perfect square, there is no Natural value of d that makes {b, c, d} a Pythagorean triple.  Tanton’s challenge is impossible.

Does anyone have a different approach?

Unexpected Proof of the Pythagorean Theorem

Following is a neat discovery of an alternative proof of the Pythagorean Theorem resulting from the multiple solutions to the Circle and Square problem.  I’m sure someone has seen this before, as there are literally 100s of unique proofs of the Pythagorean Theorem, but this one was new to me.

The intersecting chord relationships in a circle can be proven using only similar triangles.  Proofs of these are at the bottom of this post, if needed.  Using only those, you can prove the Pythagorean Theorem.

PROOF:

The image below–a revision of the diagram from my previous post–shows diameter DE in circle C.  Chord AB is a side of the given square from the Circle and Square problem and is bisected by symmetry into two segments, each of length a.  Let  r  be the radius of circle C.  Let the portion of DE from point C to chord AB have length b.  Because AB is a chord bisected by diameter DE, two right triangles are created, as shown.

AB and DE are intersecting chords, so .  Expanding the right side and moving the term to the other side gives the Pythagorean Theorem.

Short and sweet once the chord relationships are established.

SUPPORTING PROOF 1:

In the image below, AB and CD are any two chords intersecting at point E.  Vertical angles give .  Because and are inscribed angles sharing arc AC, they are also congruent.

That means , which gives , or .  QED

SUPPORTING PROOF 2:
Show that if a diameter bisects a chord, the diameter and chord are perpendicular.  Start with the vertical diameter of circle C bisecting chord AB.

It should be straightforward to show by SSS.  That means  corresponding angles ; as they also from a linear pair, those angles are both right, and the proof is established.

Two Squares, Two Triangles, and some Circles

Here’s another fun twist on another fun problem from the Five Triangles ‘blog.  A month ago, this was posted.

What I find cool about so many of the Five Triangles problems is that most permit multiple solutions.  I also like that several Five Triangles problems initially appear to not have enough information.  This one is no different until you consider the implications of the squares.

I’ve identified three unique ways to approach this problem.  I’d love to hear if any of you see any others.  Here are my solutions in the order I saw them.  The third is the shortest, but all offer unique insights.

Method 1: Law of Cosines

This solution goes far beyond the intended middle school focus of the problem, but it is what I saw first.  Sometimes, knowing more gives you additional insights.

Because DEF is a line and EF is a diagonal of a square, I know , and therefore .   is a 45-45-90 triangle with hypotenuse 6, so its leg, CE has measure .  Knowing two sides and an angle in means I could apply the Law of Cosines.

Because I’m looking for the area of ABCD,  and that is equivalent to , I don’t need to solve for the length of DC to know the area I seek is 58.

Method 2: Use Technology

I doubt many would want to solve using this approach, but if you don’t see (or know) trigonometry, you could build a solution from scratch if you are fluent with dynamic geometry software (GeoGebra, TI-Nspire, GSP).  My comfort with this made finding the solution via construction pretty straight-forward.

1. Construct segment EF with fixed length 6.
2. Build square CEGF with diagonal EF.  (This can be done several ways.  I was in a transformations mood, so I rotated EF  to get the other endpoints.)
3. Draw line EF  and then circle E with radius 4 through point E.
4. Mark point D as the intersection of circle E and line EF outside CEGF .
5. Draw a segment through points D and C.  (The square of the length of CD is the answer, but I decided to go one more step.)
6. Construct square ABCD with sides congruent to CD.  (Again, there are several ways to do this.  I left my construction marks visible in my construction below.)
7. Compute the area of ABCD.

Here is my final GeoGebra construction.

Method 3: The Pythagorean Theorem

Sometimes, changing a problem can make it much easier to solve.

As soon as I saw the problem, I forwarded it to some colleagues at my school.  Tatiana wrote back with a quick solution.  In the original image, draw diagonal, CG, of square CEGF. Because the diagonals of a square perpendicularly bisect each other, that creates right with legs 3 and 7.  That means the square of the hypotenuse of  (and therefore the area of the square) can be found via the Pythagorean Theorem.

Method 4: Coordinate Geometry

OK, I said three solutions, and perhaps this approach is completely redundant given the Pythagorean Theorem in the last approach, but you could also find a solution using coordinate geometry.

Because the diagonals of a square are perpendicular, you could construct ECFG with its center at the origin.  I placed point C at (0,3) and point E at (3,0).  That means point D is at (7,0), making the solution to the problem the square of the length of the segment from (0,3) to (7,0).  Obviously, that can be done with the Pythagorean Theorem, but in the image below, I computed number i in the upper left corner of this GeoGebra window as the square of the length of that segment.

Fun.

Finding area

I follow the Five Triangles ‘blog for cool math problems.  A recent one proved particularly nice.

At first I wasn’t sure this situation was invariant.  I didn’t see how fixing three triangle areas guaranteed a fixed quadrilateral area.  Not seeing an immediate general solution approach, I reasoned that if there was a solution, it worked for multiple overall configurations.  If it worked in general, then it must also work for any particular case I chose, so I made the cevians perpendicular.  That made each of the given area triangles right.  I modeled that by constructing the overall triangle with the cevian intersection at the origin and the legs of the given area triangles along the coordinate axes.

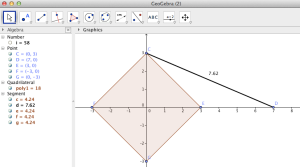
There are many ways to do this, but I reasoned that if there was a single answer, then any one of them would work.  A right triangle with legs of length 8 and 5 would have area 20.  Constructing that triangle in GeoGebra fixed the lengths of the legs of the other two triangles and the hypotenuses of the area 8 & 15 triangles intersected at a Quadrant II point.  Here’s my construction.

I  overlayed a polygon to create the quadrilateral and measured its area directly.  For fun, I also wrote algebraic equations for lines CB and DA, found the coordinates of point F by solving the 2×2 linear system, used that to derive the area of , and determined the area of the quadrilateral from that.

While I realized that this approach was just a single case of the given problem, it absolutely convinced me that the solution was unique.  Once the area 20 triangle was defined (whether or not the triangle was right), a side and the area of each of the other two given triangles is known.  That meant the heights of the triangles would be determined and thereby the location of the quadrilateral’s fourth vertex.  So, I knew without a doubt that the unknown area was , but I didn’t know a general solution.

Chronology of the General Solution

While I worked more on the problem, I also pitched it to my Twitter network and asked a colleague at my school, Tatiana Yudovina, if she was interested in the problem.  Next is Tatiana’s initial solution, followed by my generic Geogebra construction, and a much shorter solution Tatiana created.  My conclusion takes the problem to a more generic state and raises some potential extensions.

Tatiana’s First Solution:

Leveraging the fact that triangles with the same base have equivalent height and area ratios, she created a system of equations that solved to eventually determine the quadrilateral’s area.

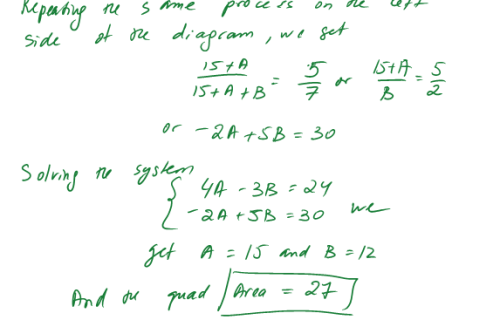
My Generic GeoGebra Solution:

While Tatiana was working on her algebraic answer, I was creating  a dynamic version on GeoGebra.  I built the area 20 triangle by first drawing a segment AB and measuring its length, a.  That meant the height of this triangle, h, was given by 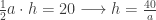. Then I constructed a perpendicular line to AB and used the “Segment with Fixed Length” tool and defined the length using the generic length of h as defined above to create segment AC.  This worked because GeoGebra defined the length of AB as a variable as shown below.

I used the “Compass” tool to create a circle with radius AC through the perpendicular line created earlier. Point D is the intersection of the circle and the normal line.  I then constructed a perpendicular to AD through D and placed a random point E on this new line.  Point E was the requisite height above AB to guarantee that 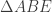always had area 20 which I confirmed by drawing the triangle and computing its area.

I hid AC, the circle, and both normals.  Segment AB was a completely independent object, and point E was free to move along the second “height” normal.  I measured AE and repeated the previous construction to create the area 15 triangle. Because BE was part of a cevian, I drew line BE to determine point J on the normal defining the final vertex of the area 15 triangle.

Again, I hid all of my constructions and repeated the process to create the final vertex, K, of the area 8 triangle off side BE of the area 20 triangle.  Extending segments AJ and BK defined point L, the final vertex of the quadrilateral.  Laying a quadrilateral in the figure let me compute its area.  Moving points A, B, and E around the screen and seeing the areas remain fixed is pretty compelling evidence that the quadrilateral’s area is always 27, and Tatiana’s proof showed why.  You can play with my final construction on GeoGebra Tube here.

Then Tatiana emailed me a much shorter proof.

Tatiana’s Short Solution:

Reversing the logic of her first solution, Tatiana reasoned that equivalent-altitude triangles had equal base and area ratios.

And the sum of X and Y gave the quadrilateral’s area.

Conclusion:

This problem was entertaining both in the solution and the multiple ways we found it.  Creating the dynamic construction gave  insights into the critical features of the problem.

Here are some potential extensions I developed for this problem.  I haven’t fully explored any of them yet, hoping some of my geometry students this year might take up the exploration challenge.  I’d love to hear if any of my readers have any further suggestions.

1. It might be interesting to create an even more dynamic construction with the areas of the three given triangles defined by sliders.
2. Can the quadrilateral’s area be expressed as a closed-form function of the areas of the three given triangles.
3. What happens on the boundaries of this problem?  That is, what happens if one of the side triangles was a degenerate with area 0? What would happen to the quadrilateral? Would would be the corresponding affect on the area formula from extension 2?
4. Extending 3 even further, if both given side triangles were degenerates with area 0, it seems that the area formula from extension 2 should collapse to the area of the final given non-zero triangle, but does it?

Thanks again, Five Triangles, for another great problem!

Transformations II and a Pythagorean Surprise

In my last post, I showed how to determine an unknown matrix for most transformations in the xy-plane and suggested that they held even more information.

Given a pre-image set of points which can be connected to enclose one or more areas with either clockwise or counterclockwise orientation.  If a transformation T represented by matrix is applied to the pre-image points, then the determinant of , , tells you two things about the image points.

1. The area enclosed by similarly connecting the image points is times the area enclosed by the pre-image points, and
2. The orientation of the image points is identical to that of the pre-image if , but is reversed if .  If , then the image area is 0 by the first property, and any question about orientation is moot.

In other words, is the area scaling factor from the pre-image to the image (addressing the second half of CCSSM Standard NV-M 12 on page 61 here), and the sign of indicates whether the pre-image and image have the same or opposite orientation, a property beyond the stated scope of the CCSSM.

Example 1: Interpret for the matrix representing a reflection over the x-axis, .

From here, .  The magnitude of this is 1, indicating that the area of an image of an object reflected over the line is 1 times the area of the pre-image—an obviously true fact because reflections preserve area.

Also, indicating that the orientation of the reflection image is reversed from that of its pre-image.  This, too, must be true because reflections reverse orientation.

Example 2: Interpret for the matrix representing a scale change that doubles x-coordinates and triples y-coordinates, .

For this matrix, , indicating that the image’s area is 6 times that of its pre-image area, while both the image and pre-image have the same orientation.  Both of these facts seem reasonable if you imagine a rectangle as a pre-image.  Doubling the base and tripling the height create a new rectangle whose area is six times larger.  As no flipping is done, orientation should remain the same.

Example 3 & a Pythagorean Surprise:  What should be true about   for the transformation matrix representing a generic rotation of units around the origin,   ?

Rotations preserve area without reversing orientation, so should be +1.  Using this fact and computing the determinant gives

.

In a generic right triangle with hypotenuse C, leg A adjacent to acute angle , and another leg B, this equation is equivalent to , or , the Pythagorean Theorem.  There are literally hundreds of proofs of this theorem, and I suspect this proof has been given sometime before, but I think this is a lovely derivation of that mathematical hallmark.

Conclusion:  While it seems that these two properties about the determinants of transformation matrices are indeed true for the examples shown, mathematicians hold out for a higher standard.   I’ll offer a proof of both properties in my next post.