Value Process over Answers

Most of my thinking about teaching lately has been about the priceless, timeless value of process in problem solving over the ephemeral worth of answers.  While an answer to a problem puts a period at the end of a sentence, the beauty and worth of the sentence was the construction, word choice, and elegance employed in sharing the idea at the heart of the sentence.

Just as there are many ways to craft a sentence–from cumbersome plodding to poetic imagery–there are equally many ways to solve problems in mathematics.  Just as great writing reaches, explores, and surprises, great problem solving often starts with the solver not really knowing where the story will lead, taking different paths depending on the experience of the solver, and ending with even more questions.

I experienced that yesterday reading through tweets from one of my favorite middle and upper school problem sources, Five Triangles.  The valuable part of what follows is, in my opinion, the multiple paths I tried before settling on something productive.  My hope is that students learn the value in exploration, even when initially unproductive.

At the end of this post, I offer a few variations on the problem.

The Problem

Try this for yourself before reading further.  I’d LOVE to hear others’ approaches.

First Thoughts and Inherent Variability

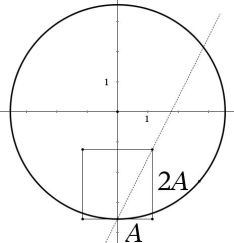
My teaching career has been steeped in transformations, and I’ve been playing with origami lately, so my brain immediately translated the setup:

Fold vertex A of equilateral triangle ABC onto side BC.  Let segment DE be the resulting crease with endpoints on sides AB and AC with measurements as given above.

So DF is the folding image of AD and EF is the folding image of AE.  That is, ADFE is a kite and segment DE is a perpendicular bisector of (undrawn) segment AF.  That gave  .

I also knew that there were lots of possible locations for point F, even though this set-up chose the specific orientation defined by BF=3.

Lovely, but what could I do with all of that?

Trigonometry Solution Eventually Leads to Simpler Insights

Because FD=7, I knew AD=7.  Combining this with the given DB=8 gave AB=15, so now I knew the side of the original equilateral triangle and could quickly compute its perimeter or area if needed.  Because BF=3, I got FC=12.

At this point, I had thoughts of employing Heron’s Formula to connect the side lengths of a triangle with its area.  I let AE=x, making EF=x and .  With all of the sides of defined, its perimeter was 27, and I could use Heron’s Formula to define its area:

But I didn’t know the exact area, so that was a dead end.

Since is equilateral, , I then thought about expressing the area using trigonometry.  With trig, the area of a triangle is half the product of any two sides multiplied by the sine of the contained angle.  That meant .

Now I had two expressions for the same area, so I could solve for x.

Squaring both sides revealed a quadratic in x.  I could do this algebra, if necessary, but this was clearly a CAS moment.

I had two solutions, but this felt WAY too complicated.  Also, Five Triangles problems are generally accessible to middle school students.  The trigonometric form of a triangle’s area is not standard middle school fare.  There had to be an easier way.

A Quicker Ending

Thinking trig opened me up to angle measures.  If I let , then , making , and I suddenly had my simple breakthrough!  Because their angles were congruent, I knew .

Because the triangles were similar, I could employ similarity ratios.

And that is one of the CAS solutions by a MUCH SIMPLER approach.

Extensions and Variations

Following are five variations on the original Five Triangles problem.  What other possible variations can you find?

1)  Why did the CAS give two solutions?  Because had all three sides explicitly given, by SSS there should be only one solution.  So is the 13.0714 solution real or extraneous?  Can you prove your claim?  If that solution is extraneous, identify the moment when the solution became “real”.

2)  Eliminating the initial condition that BF=3 gives another possibility.  Using only the remaining information, how long is ?

now has SSA information, making it an ambiguous case situation.  Let BF=x and invoke the Law of Cosines.

Giving the original BF=3 solution and a second possible answer:  BF=5.

3)  You could also stay with the original problem asking for AE.

From above, the solution for BF=3 is AE=10.5.  But if BF=5 from the ambiguous case, then FC=10 and the similarity ratio above becomes

4)  Under what conditions is ?

5)  Consider all possible locations of folding point A onto .  What are all possible lengths of ?

 

 

Circle and Square

Here’s another great geometry + algebra problem, posed by Megan Schmidt and pitched by Justin Aion to some students in his Geometry class.

Following is the problem as Justin posed it yesterday.

Justin described the efforts of three of his students’ on his his ‘blog.  Following is my more generalized approach.  Don’t read further if you want to solve this problem for yourself!

SOLUTION ALERT!!!

My first instinct in any case like this is build it in a dynamic geometry package and play.  Using my TI-Nspire, without loss of generality, I graphed a circle centered at the origin, constructed a tangent segment at the bottom of the circle centered on the y-axis, and then used that segment to construct a square.  I recognized that the locus of the upper right corners of all such squares would form a line.

That made it clear to me that for any circle, there was a unique square that intersected the circle three times as Megan had posed.

Seeing this and revealing its algebraic bias, my mind conceived an algebraic solution.  Assuming the radius of the circle is R, the equation of my circle is making the lower y-intercept of the circle .  That made the locus line containing the upper right corner of the square.

To find generic coordinates of the upper right corner of the square in terms of R, I just needed to solve the system of equations containing the circle and the line.  That’s easy enough to compute by hand if you can handle quadratic algebra.  That manipulation is not relevant right now, so my Nspire CAS’s version is:

The output confirms the two intersections are  and the unknown at .

Because of the horizontal symmetry of the square with respect to the y-axis, the system solution shows that the generic length of the side of the square is .  The circle’s y-intercept at means the generic diameter of the circle is .

Therefore, the generic ratio of the circle’s diameter to the square’s side length is

.

And this is independent of the circle’s radius!  The diameter of the circle is always of the square’s side.

CONCLUSION:

For Megan’s particular case with a side length of 20, that gives a circle diameter of 25, confirming Justin’s students’ solution.

Does anyone have a different approach?  I’m happy to compile and share all I get.

AN ASIDE:

While not necessary for the generalized solution, it was fun to see a 3-4-5 right triangle randomly appear in Quadrant 1.

Common numerators

As long as I’m leveraging Five Triangles posts, here is another recent one worth discussing.

Too often, I think students believe that the only way to compare fractions is to find common denominators.  In this problem, three of the four given denominators are big enough primes that the common denominator approach would result in some painful enough by-hand computations.

But the pattern in the numerators screams for attention.  Why not find some common numerators and compare the fractions that way?  That approach cracks the problem pretty efficiently.

As a bonus, the common numerator approach also shows that the four given fractions are surprisingly close to each other in size.

Keep thinking …

Two Squares, Two Triangles, and some Circles

Here’s another fun twist on another fun problem from the Five Triangles ‘blog.  A month ago, this was posted.

What I find cool about so many of the Five Triangles problems is that most permit multiple solutions.  I also like that several Five Triangles problems initially appear to not have enough information.  This one is no different until you consider the implications of the squares.

I’ve identified three unique ways to approach this problem.  I’d love to hear if any of you see any others.  Here are my solutions in the order I saw them.  The third is the shortest, but all offer unique insights.

Method 1: Law of Cosines

This solution goes far beyond the intended middle school focus of the problem, but it is what I saw first.  Sometimes, knowing more gives you additional insights.

Because DEF is a line and EF is a diagonal of a square, I know , and therefore .   is a 45-45-90 triangle with hypotenuse 6, so its leg, CE has measure .  Knowing two sides and an angle in means I could apply the Law of Cosines.

Because I’m looking for the area of ABCD,  and that is equivalent to , I don’t need to solve for the length of DC to know the area I seek is 58.

Method 2: Use Technology

I doubt many would want to solve using this approach, but if you don’t see (or know) trigonometry, you could build a solution from scratch if you are fluent with dynamic geometry software (GeoGebra, TI-Nspire, GSP).  My comfort with this made finding the solution via construction pretty straight-forward.

1. Construct segment EF with fixed length 6.
2. Build square CEGF with diagonal EF.  (This can be done several ways.  I was in a transformations mood, so I rotated EF  to get the other endpoints.)
3. Draw line EF  and then circle E with radius 4 through point E.
4. Mark point D as the intersection of circle E and line EF outside CEGF .
5. Draw a segment through points D and C.  (The square of the length of CD is the answer, but I decided to go one more step.)
6. Construct square ABCD with sides congruent to CD.  (Again, there are several ways to do this.  I left my construction marks visible in my construction below.)
7. Compute the area of ABCD.

Here is my final GeoGebra construction.

Method 3: The Pythagorean Theorem

Sometimes, changing a problem can make it much easier to solve.

As soon as I saw the problem, I forwarded it to some colleagues at my school.  Tatiana wrote back with a quick solution.  In the original image, draw diagonal, CG, of square CEGF. Because the diagonals of a square perpendicularly bisect each other, that creates right with legs 3 and 7.  That means the square of the hypotenuse of  (and therefore the area of the square) can be found via the Pythagorean Theorem.

Method 4: Coordinate Geometry

OK, I said three solutions, and perhaps this approach is completely redundant given the Pythagorean Theorem in the last approach, but you could also find a solution using coordinate geometry.

Because the diagonals of a square are perpendicular, you could construct ECFG with its center at the origin.  I placed point C at (0,3) and point E at (3,0).  That means point D is at (7,0), making the solution to the problem the square of the length of the segment from (0,3) to (7,0).  Obviously, that can be done with the Pythagorean Theorem, but in the image below, I computed number i in the upper left corner of this GeoGebra window as the square of the length of that segment.

Fun.

Systems of lines

Here’s an interesting variation of a typical (MS) problem I found by following the Five Triangles ‘blog: http://fivetriangles.blogspot.com/2013/09/97-no-triangle.html .

(Note:  If you sign up on this or other ‘blogs, you can get lots of problems emailed to you every time they are added.)

INITIAL SOLUTION

I know this question can absolutely be solved without using technology, but when a colleague asked if it was appropriate to use technology here (my school is one-to-one with tablet laptops), I thought it would be cool to share with her the ease and power of Desmos.  You can enter the equations from the problem exactly as given (no need to solve for y), or you can set up a graph in advance for your students and email them a direct link to an already-started problem.

If you follow this link, you can see how I used a slider (a crazy-simple addition on Desmos) to help students discover the missing value of a.

FOLLOW-UP

I suggest in this case that playing with this problem graphically would grant insight for many students into the critical role (for this problem) of the intersection point of the two explicitly defined lines.  With or without technology support, you could then lead your students to determine the coordinates of that intersection point and thereby the value of a.

Keeping with my CAS theme, you could determine those coordinates using GeoGebra’s brand new CAS View:

Substituting the now known values of x and y into the last equation in the problem gives the desired value of a.

NOTE:  I could have done the sliders in GeoGebra, too, but I wanted to show off the ease of my two favorite (and free!) online math tools.

CONCLUSION

Thoughts?  What other ideas or problems could be enhanced by a properly balanced use of technology?

As an extension to this particular problem, I’m now wondering about the area of triangle formed for any value of a.  I haven’t played with it yet, but it looks potentially interesting.  I see both tech and non-tech ways to approach it.

Finding area

I follow the Five Triangles ‘blog for cool math problems.  A recent one proved particularly nice.

At first I wasn’t sure this situation was invariant.  I didn’t see how fixing three triangle areas guaranteed a fixed quadrilateral area.  Not seeing an immediate general solution approach, I reasoned that if there was a solution, it worked for multiple overall configurations.  If it worked in general, then it must also work for any particular case I chose, so I made the cevians perpendicular.  That made each of the given area triangles right.  I modeled that by constructing the overall triangle with the cevian intersection at the origin and the legs of the given area triangles along the coordinate axes.

There are many ways to do this, but I reasoned that if there was a single answer, then any one of them would work.  A right triangle with legs of length 8 and 5 would have area 20.  Constructing that triangle in GeoGebra fixed the lengths of the legs of the other two triangles and the hypotenuses of the area 8 & 15 triangles intersected at a Quadrant II point.  Here’s my construction.

I  overlayed a polygon to create the quadrilateral and measured its area directly.  For fun, I also wrote algebraic equations for lines CB and DA, found the coordinates of point F by solving the 2×2 linear system, used that to derive the area of , and determined the area of the quadrilateral from that.

While I realized that this approach was just a single case of the given problem, it absolutely convinced me that the solution was unique.  Once the area 20 triangle was defined (whether or not the triangle was right), a side and the area of each of the other two given triangles is known.  That meant the heights of the triangles would be determined and thereby the location of the quadrilateral’s fourth vertex.  So, I knew without a doubt that the unknown area was , but I didn’t know a general solution.

Chronology of the General Solution

While I worked more on the problem, I also pitched it to my Twitter network and asked a colleague at my school, Tatiana Yudovina, if she was interested in the problem.  Next is Tatiana’s initial solution, followed by my generic Geogebra construction, and a much shorter solution Tatiana created.  My conclusion takes the problem to a more generic state and raises some potential extensions.

Tatiana’s First Solution:

Leveraging the fact that triangles with the same base have equivalent height and area ratios, she created a system of equations that solved to eventually determine the quadrilateral’s area.

My Generic GeoGebra Solution:

While Tatiana was working on her algebraic answer, I was creating  a dynamic version on GeoGebra.  I built the area 20 triangle by first drawing a segment AB and measuring its length, a.  That meant the height of this triangle, h, was given by . Then I constructed a perpendicular line to AB and used the “Segment with Fixed Length” tool and defined the length using the generic length of h as defined above to create segment AC.  This worked because GeoGebra defined the length of AB as a variable as shown below.

I used the “Compass” tool to create a circle with radius AC through the perpendicular line created earlier. Point D is the intersection of the circle and the normal line.  I then constructed a perpendicular to AD through D and placed a random point E on this new line.  Point E was the requisite height above AB to guarantee that always had area 20 which I confirmed by drawing the triangle and computing its area.

I hid AC, the circle, and both normals.  Segment AB was a completely independent object, and point E was free to move along the second “height” normal.  I measured AE and repeated the previous construction to create the area 15 triangle. Because BE was part of a cevian, I drew line BE to determine point J on the normal defining the final vertex of the area 15 triangle.

Again, I hid all of my constructions and repeated the process to create the final vertex, K, of the area 8 triangle off side BE of the area 20 triangle.  Extending segments AJ and BK defined point L, the final vertex of the quadrilateral.  Laying a quadrilateral in the figure let me compute its area.  Moving points A, B, and E around the screen and seeing the areas remain fixed is pretty compelling evidence that the quadrilateral’s area is always 27, and Tatiana’s proof showed why.  You can play with my final construction on GeoGebra Tube here.

Then Tatiana emailed me a much shorter proof.

Tatiana’s Short Solution:

Reversing the logic of her first solution, Tatiana reasoned that equivalent-altitude triangles had equal base and area ratios.

And the sum of X and Y gave the quadrilateral’s area.

Conclusion:

This problem was entertaining both in the solution and the multiple ways we found it.  Creating the dynamic construction gave  insights into the critical features of the problem.

Here are some potential extensions I developed for this problem.  I haven’t fully explored any of them yet, hoping some of my geometry students this year might take up the exploration challenge.  I’d love to hear if any of my readers have any further suggestions.

1. It might be interesting to create an even more dynamic construction with the areas of the three given triangles defined by sliders.
2. Can the quadrilateral’s area be expressed as a closed-form function of the areas of the three given triangles.
3. What happens on the boundaries of this problem?  That is, what happens if one of the side triangles was a degenerate with area 0? What would happen to the quadrilateral? Would would be the corresponding affect on the area formula from extension 2?
4. Extending 3 even further, if both given side triangles were degenerates with area 0, it seems that the area formula from extension 2 should collapse to the area of the final given non-zero triangle, but does it?

Thanks again, Five Triangles, for another great problem!

Arrangements Connections for Young Students

Mathematics is not arithmetic.

The latter is a set of symbol manipulation rules that dominates most of what we teach in school.  Mathematics, on the other hand, is a science of patterns.  It is a way of logical thinking, making sense of forms and arrangements–sometimes applied and sometimes purely imagined.  It involves looking at the implications of what we know and pushing that knowledge as far as we can to see what else can be learned based solely upon connections we can make from our assumptions.

Within the last few weeks, I’ve discovered a great daily ‘blog run by @Five_Triangles “for (but not limited to) school years 6-8.”  I’d argue that those posts are great for a broader range of ages. I gave my 3rd grade daughter one of the puzzles during breakfast.  We had some great conversations then and on the way to school.  I share those below.  Another offering extends that thinking in a way that may not be immediately obvious to young people.

Here’s the part of the post I used at breakfast.

For my daughter, I saw this problem presenting two different possibilities–the obvious arithmetic problem and a mathematics extension.  The arithmetic requires very basic subtraction facts and wee bit of trial-and-error (a GREAT mathematics skill!) to tease out a solution.  Part of the mathematics here, in my opinion, involves asking a “What if?” question.

I posed this problem to my 3rd grade daughter and after randomly dropping in some numbers at first and seeing some frustration, I said to her, “I wonder what sorts of numbers subtract to give 3.”  Her frustration evaporated as she started making a list of several possibilities for such digits. She noted that there were far more possibilities for these difference than space in the problem allowed.  I encouraged her to keep trying.  We never explicitly discussed the problem’s set up with a four-digit number subtracted from a five-digit number, but I saw her try a couple different first digits before realizing that the first character of the five-digit number clearly had to be “1”.  A little more experimentation and she had an answer.

She thought the puzzle was over–after all, school has trained her to think that once she had “an” answer, she must have found “the” answer.

That’s when I prompted some mathematics.  I asked if she could find another answer.  A few other prompts and she had found 6 different solutions.  I asked her how she found them.  “Easy,” she replied.  “You just put the number pairs in different orders.”  She found through trial-and-error that the five-digit number always started “12…” and therefore the four-digit number started “9…”.  Checking her list of differences leading to 3 left no other possibilities.  Everything else was flexible, thus her six different answers.

• Can you explain why the five-digit number must start “12…”?
• Once I had the “12…” and “9…”, I knew there were at least 6 solutions  before I had found even the first one.  My daughter wasn’t ready for this thought, but can you explain why this is true?
• Can you find all 6 answers?
• Better: Can you explain why there cannot be any more?

The second part of the problem (with the same rules and a different result) is definitely tougher.

You can quickly conclude that the first digit of the five-digit number must be 4 or 3, but it’s definitely more challenging to tease out the rest.  Rather than dealing with the entire problem at once, I suggest another great mathematics strategy:  Simplify the problem.  Using only the digits 1 to 9, can you find all possibilities that would result in the beginning of the problem?

If this is part of an answer, the six digits not used in those three boxes must have an arrangement that subtracts to 333.  Unfortunately, none of these actually pan out.  Convince yourself why this must be true.  Students need to learn that not finding an answer is OK.  Knowing that there’s not a solution is actually a solution–you’ve learned something.

Extending the beginning of the problem to

eventually shows that the five-digit number could start “412..” with the four-digit number starting “79..”.  That means the remaining four digits must have exactly two arrangements for precisely the same reasons that the first problem had six solutions.  Can you find the two arrangements that satisfy the 33333 problem?  In case you want to check, I list the answers at the end of this post.

The next week provided another puzzle using the arrangements idea.

The problem doesn’t yield a straightforward solution that can be solved.  Instead, laying out all possible finishing arrangements and testing the veracity of the claims leads to a solution.  Again, there are three entries, so this problem is (mathematically) just like the 3333 subtraction problem above–both have six possible arrangements.  Helping a young person see this connection would be a great thought achievement.

Start by listing the six possible 1st, 2nd, and 3rd place arrangements of the letters A, B, and C:  A-B-C, A-C-B, B-A-C, B-C-A, C-A-B, & C-B-A.   As an example, if the boys finished A-B-C, all three boys would have told the truth, so that finish doesn’t satisfy the problem requirement of one false statement.  Comparing each arrangement to the boys’ statements eventually shows that only one of these arrangements satisfies the problem’s requirement that exactly one of the three boys made a false statement.

A good mathematical extension would be to see if there are any other questions that could be asked from the boys’ statements.  Is it possible that all three told the truth?  Is it possible that only one was truthful?  Are there any other possible outcomes?  Do any of these have unique outcomes given the boys’ statements, or do some have multiple possibilities?

CONCLUSION:  I fear that too often school and students stop at a single answer and don’t explore other possibilities.  Asking “What if” is a critical question in all of science and mathematics.  It inspires creativity, wonder, and exploration.  It doesn’t always yield results, so it also helps motivate stamina.  Convincing yourself that there are no (more) solutions is itself an intellectual accomplishment.

We need more of this.

SOLUTIONS:

• 3333 solutions: 12678-9345, 12687-9354, 12768-9435, 12786-9453, 12867-9534, & 12876-9543.
• 33333 solutions: 41268-7935 & 41286-7953.
• Competition solution:  A-C-B