Inscribed Right Angle Proof Without Words

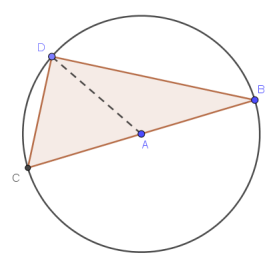
Earlier this past week, I assigned the following problem to my 8th grade Geometry class for homework.  They had not explored the relationships between circles and inscribed angles, so I added dashed auxiliary segment AD as a hint.

What follows first is the algebraic solution I expected most to find and then an elegant transformational explanation one of my students produced.

PROOF 1:

Given circle A with diameter BC and point D on the circle.  Prove triangle BCD is a right triangle.

After some initial explorations on GeoGebra sliding point D around to discover that its angle measure was always independent of the location of D, most successful solutions recognized congruent radii AB, AC, and AD, creating isosceles triangles CAD and BAD.  That gave congruent base angles x in triangle CAD, and y in BAD.

The interior angle sum of a triangle gave , or , confirming that BCD was a right triangle.

PROOF 2:

Then, one student surprised us.  She marked the isosceles base angles as above before rotating about point A.

Because the diameter rotated onto itself, the image and pre-image combined to form an quadrilateral with all angles congruent.  Because every equiangular quadrilateral is a rectangle, M had confirmed BCD was a right triangle.

CONCLUSION:

I don’t recall seeing M’s proof before, but I found it a delightfully elegant application of quadrilateral properties.  In my opinion, her rotation is a beautiful proof without words solution.

Encourage freedom, flexibility of thought, and creativity, and be prepared to be surprised by your students’ discoveries!