Painting and Probability

Posted on March 31, 2018 | Leave a comment

 

Here’s a cool probability problem the start of which is accessible to middle and high school students with careful reasoning.  It was posted by Alexander Bogomolny on Cut the Knot a week ago. I offer what I think is a cool extension of the problem following the initial credits.

The next day Mike Lawler tweeted another phenomenal video solution worked out with his boys during Family Math.

Mike’s videos show his boys thinking through simpler discrete cases of the problem and their eventual case-by-case solution to the nxnxn question.  The last video on the page gives a lovely alternative solution completely bypassing the case-by-case analyses.  This is also “Solution 1” on Alexander’s page.

EXTENDING THE PROBLEM:

When I first encountered the problem, I wanted to think about it before reading any solutions.  As with Mike’s boys, I was surprised early on when the probability for a 2x2x2 cube was \displaystyle \frac{1}{2} and the probability for a 3x3x3 cube was \displaystyle \frac{1}{3}.  That was far too pretty to be a coincidence.  My solution exactly mirrored the nxnxn case-by-case analysis in Mike’s videos:  the probability of rolling a painted red face up from a randomly selected smaller cube is \displaystyle \frac{1}{n}.

Surely something this simple and clean could be generalized.  Since a cube can be considered a “3-dimensional square”, I re-phrased Alexander’s question into two dimensions.  The trickier part was thinking what it would mean to “roll” a 2-dimensional shape.

The outside of an nxn square is painted red and is chopped into n^2 unit squares.  The latter are thoroughly mixed up and put into a bag.  One small square is withdrawn at random from the bag and spun on a flat surface.  What is the probability that the spinner stops with a red side facing you?

Shown below is a 4×4 square, but in all sizes of 2-dimensional squares, there are three possible types in the bag:  those with 2, 1, or 0 sides painted.

Square1

I solved my first variation case by case.  In any nxn square,

  • There are 4 corner squares with 2 sides painted.  The probability of picking one of those squares and then spinning a red side is \displaystyle \frac{4}{n^2} \cdot \frac{2}{4} = \frac{2}{n^2}.
  • There are 4(n-2) edge squares not in a corner with 1 side painted.  The probability of picking one of those squares and then spinning a red side is \displaystyle \frac{4(n-2)}{n^2} \cdot \frac{1}{4} = \frac{n-2}{n^2}.
  • All other squares have 0 sides painted, so the probability of picking one of those squares and then spinning a red side is 0.
  • Adding the probabilities for the separate cases gives the total probability:  \displaystyle \frac{2}{n^2}+\frac{n-2}{n^2}=\frac{1}{n}

After reading Mike’s and Alexander’s posts, I saw a much easier approach.

  • Paint all 4 edges of an nxn square, and divide each painted edge into n painted unit segments.  This creates 4 \cdot n total painted small segments.
  • Decompose the nxn original square into n^2 unit squares.  Each unit square has 4 edges giving 4 \cdot n^2 total edges.
  • Because every edge of every unit square is equally likely to be spun, the total probability of randomly selecting a smaller square and spinning a red side is \displaystyle \frac{4n}{4n^2}=\frac{1}{n}.

The dimensions of the “square” don’t seem to matter!

WARNING: 

Oliver Wendell Holmes noted, “A mind that is stretched by a new experience can never go back to its old dimensions.”  The math after this point has the potential to stretch…

EXTENDING THE PROBLEM MORE:

I now wondered whether this was a general property.

In the 2-dimensional square, 1-dimensional edges were painted and the square was spun to find the probability of a red edge facing.  With the originally posed cube, 2-dimensional faces were painted and the cube was tossed to find the probability of an upward-facing red face.  These cases suggest that when a cube of some dimension with edge length n is painted, is decomposed into unit cubes of the original dimension, and is spun/tossed to show a cube of one smaller dimension, then the probability of getting a painted smaller-dimensional cube of is always \displaystyle \frac{1}{n}, independent of the dimensions occupied by the cube.

Going beyond the experiences of typical middle or high school students, I calculated this probability for a 4-dimensional hypercube (a tesseract).

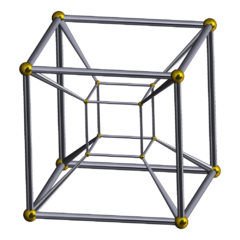
  • The exterior of a tesseract is 8 cubes.  Ignore the philosophical difficulty of what it means to “paint” (perhaps fill?) an entire cube.  After all, we’re already beyond the experience of our 3-dimensions.
  • Paint/fill all 8 cubes on the surface of the tesseract, and divide each painted cube into n^3 painted unit cubes.  This creates 8 \cdot n^3 total painted unit cubes.
  • Decompose the original tesseract into n^4 unit tesseracts.  Each unit tesseract has 8 cubes giving 8 \cdot n^4 total unit cubes.
  • Because every unit cube on every unit tesseract is equally likely to be “rolled”, the total probability of randomly selecting a smaller tesseract and rolling a red cube is \displaystyle \frac{8n^3}{8n^4}=\frac{1}{n}.

The probability is independent of dimension! 

More formally,

The exterior of a d-dimensional hypercube with edge length n is painted red and is chopped into n^d unit d-dimensional hypercubes.  The latter are put into a bag of sufficient dimension to hold them and thoroughly mixed up.  A unit d-dimensional hypercube is withdrawn at random from the bag and tossed.  The probability that the unit d-dimensional hypercube lands with a red (d-1)-dimensional hypercube showing is \displaystyle \frac{1}{n} .

PROOF:

  • The exterior of a d-dimensional hypercube is comprised of 2d (d-1)-dimensional hypercubes of dimension (d-1).  Paint/fill all 2d surface hypercubes and divide each painted (d-1)-dimensional hypercube into n^{d-1} painted unit hypercubes.  This creates 2d \cdot n^{d-1} total painted unit hypercubes.
  • Decompose the original tesseract into n^d unit d-dimensional hypercubes.  Each unit d-dimensional hypercube has 2d surface (d-1)-dimensional hypercubes giving 2d \cdot n^d total surface unit d-dimensional hypercubes.
  • Because every unit (d-1)-dimensional hypercube on the surface of every unit d-dimensional hypercube is equally likely to be “rolled”, the total probability of randomly selecting a unit d-dimensional hypercube and rolling a (d-1)-dimensional red-painted hypercube is \displaystyle \frac{2d \cdot n^{d-1}}{2d \cdot n^d}=\frac{1}{n}.

 

I hope you can now return to something close to your old dimensions.

This entry was posted in problem-solving and tagged , , , , . Bookmark the permalink.

Leave a comment