About 10 years ago, I was introducing a lesson on series in a calculus class. This course was the first for which I had a Computer Algebra System (CAS, in this case, a TI-89) in the hands of every student. I’ve learned that “off task” who are still engaged in the class are typically the most creative sources of ideas.
In this case, I was using the CAS as a support and verification tool on a lesson reviewing geometric series and introducing the harmonic series. At the end of class, a student approached me with his CAS in hand and an intensely puzzled look on his face. He asked, “How did this happen?” and showed me his calculator screen.
Note the power of the CAS in this instance to handle way more math than the student understood, but it definitely piqued his interest and mine with its handling of an infinite bound, and especially for they completely unexpected appearance of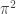 
. What in the world was going on here? Surely there must be some error.
I had no clue, but promised to get back to him within the next few days. After a week of trying to solve it on my own and not really knowing to engage a network for help, I humbly returned to my student and confessed that I simply didn’t have an answer for him even though the problem looked amazingly cool. I played with the problem off-and-on over the ensuing months until one Saturday afternoon two years later when I was reading a math article on Euler that offers his ideas on product series. [I had never studied such things. Whether my background should have been broader is an open question.]
If you don’t have the stomach or time or inclination to consume the proof that follows, please scroll to the last few paragraphs of this post for my general comments on the reach of this problem.
Spoiler Alert: If you want to explore why the series sum my student re-discovered is true, stop reading now!
The following proof may not be absolutely water-tight, but it is how I’ve come to understand Euler’s stunning solution.
If you remember Maclaurin Series from differential calculus, you might recall that the polynomial equivalent for the sine function at x=0 is 
The connection I missed for two years was that this is just a polynomial, and polynomials can be factored. OK, sine’s not really a polynomial, but if you can approximate it as an expanded polynomial (the Maclaurin series above), why can’t you do the same in factored form?
So, the x-intercepts of sine are 
and by the typical manner of writing factored polynomials today, one would write 
But polynomial factors can also be written in the slightly more complicated form, 
, which actually ends of simplifying this problem significantly.
The coefficient A allows the factor (product) series to vertically stretch to fit any curve with the given roots. Notice, too, that the equidistant terms on either side of the x term are conjugates, so the series can be further rewritten as an infinite product of differences of squares.
But now there are two polynomials representing the same function, so the polynomials must be equivalent. Therefore,
a pretty amazing equivalence in its own right.
Whenever two polynomials are equivalent, their coefficients must be equal when the polynomials are written in the same form. To explore this, you can expand the product form. Notice that the Maclaurin polynomial doesn’t have a constant term, and neither does the factored term because any combination of terms from the product eventually must multiply by the Ax term. Continuing this reasoning, the only way to get a linear term is to take the Ax term and then multiply by the 1 from every single binomial factor. Anything else would yield a term with degree higher than 1. Equating the linear terms from the product expansion (Ax) and the Maclaurin series (x) proves that A=1.
You can reason why the product series cannot produce quadratic terms, so turn your attention now to the cubic terms. The only cubic terms in the expansion of the product series come from multiplying the leading x term by a quadratic term in ONE of the binomial factors and by the 1 terms in all of the remaining binomial factors. Collecting all of these cubic terms and equating them to the known Maclaurin cubic term gives
Factoring out 
allows the coefficients to compared and a minor re-arrangement from there proves my student’s result.
I’ve always been blown away by how quickly this proof collapses from very cumbersome equations into such a beautiful result. It also amazes me that while a sine function was used to leverage the proof, the final result conveys nothing of its presence. Equating higher order terms from the two series allows you to compute the value of 
for any even values of k, but odd powers of k greater than 1 are still an outstanding problem in mathematics. We know they converge; we simply don’t have closed form values for their sums. Anyone up for the challenge?
(By the way, you can read here some historical context and connections from this problem to much more substantial mathematics today, including a connection to the zeta function which underlies the current search for a proof to the prime number theorem.)
This is some pretty heady stuff for a student who just wanted to know what happened if you tweaked an expression a little bit. But then, isn’t that how all good math starts? My only regret is that the student who initially posed the problem graduated high school before we could find the answer to his question. The positive side is that hundreds of my students since then have been able to see this gorgeous connection.
I hope all my students know that I value their questions (no matter how shallow, deep, or off-topic) and that I learn more and become a better teacher with every new perspective they share.
Post-scripts (9/5/11) from communications with David Doster: I knew that I was walking in the footsteps of others as I created the proof above on my own, but a serendipitous communication with a colleague I met at a 1993 Woodrow Wilson institute on the Mathematics of Change. David pointed me toward Robin Chapman’s Home Page which includes 14 different proofs of this result–Euler’s (and my) proof is the 7th in that list. This result has also been a favorite of William Dunham as published in his books Journey Through Genius and Euler, The Master of Us All, both definitely worth reading.
, and their CAS gave the top line of the image below.
and press the carot (^) key. Then type the integer of the derivative you want.)
, thinking that this product of odd functions leading to an even function would be a nice, but minor, extension for my students. 
as 
, the graph of 
. As shown and to my surprise, 
seemed to parallel the anticipated absolute value function instead of approaching it. Hmmmm…..
.
,
as x approaches infinity, and
. A less-obvious recognition is that as 
must behave exactly like 
because its product with x becomes 1,![\displaystyle\lim_{x\to\infty} [x*(\frac{\pi}{2}-tan^{-1}x)]\rightarrow\infty*0](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Clim_%7Bx%5Cto%5Cinfty%7D+%5Bx%2A%28%5Cfrac%7B%5Cpi%7D%7B2%7D-tan%5E%7B-1%7Dx%29%5D%5Crightarrow%5Cinfty%2A0&bg=ffffff&fg=333333&s=0&c=20201002)
chrisharrow
CAS Musings 